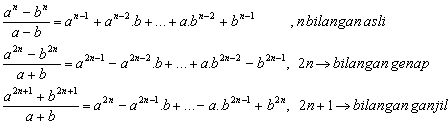Suku Banyak

Bentuk Umum

F(x) = P(x).H(x) + S(x)

F(x) = suku banyak
P(x) = pembagi
H(x) = hasil bagi
S(x) = sisa
Teorema Sisa:
Jika suatu suku banyak F(x) dibagi oleh (x – k) maka sisanya adalah F(k)
Jika pembagi berderajat n maka sisanya berderajat n – 1
Jika suku banyak berderajat m dan pembagi berderajat n, maka hasil baginya berderajat m – n
Cara Pembagian Suku Banyak
Contoh:
F(x) = 2x³ – 3x² + x + 5 dibagi dengan P(x) = 2x² – x – 1
1. Pembagian biasa

Jadi hasil baginya: H(X) = x – 1, sisanya S(x) = x + 4
2. Cara Horner/Skema
bisa digunakan untuk pembagi berderajat 1 atau pembagi yang dapat difaktorkan menjadi pembagi-pembagi berderajat 1
Cara:

• Tulis koefisiennya saja → harus runtut dari koefisien xⁿ, x^{n – 1}, … hingga konstanta (jika ada variabel yang tidak ada, maka koefisiennya ditulis 0)

Contoh: untuk 4x³ – 1, koefisien-koefisiennya adalah 4, 0, 0, dan -1 (untuk x³, x², x, dan konstanta)

• Jika koefisien derajat tertinggi P(x) ≠ 1, maka hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
• Jika pembagi dapat difaktorkan, maka:

Jika pembagi dapat difaktorkan menjadi P₁ dan P₂, maka S(x) = P₁.S₂ + S₁

Jika pembagi dapat difaktorkan menjadi P₁, P₂, P₃, maka S(x) = P₁.P₂.S₃ + P₁.S₂ + S₁

Jika pembagi dapat difaktorkan menjadi P₁, P₂, P₃, P₄, maka S(x) = P₁.P₂.P₃.S₄ + P₁.P₂.S₃ + P₁.S₂ + S₁

dan seterusnya

Untuk soal di atas,
P(x) = 2x² – x – 1 = (2x + 1)(x – 1)
P₁: 2x + 1 = 0 → x = –½
P₂: x – 1 = 0 → x = 1
Cara Hornernya:

H(x) = 1.x – 1 = x – 1
S(x) = P₁.S₂ + S₁ = (2x + 1).1/2 + 7/2 = x + ½ + 7/2 = x + 4
3. Cara koefisien tak tentu
F(x) = P(x).H(x) + S(x)
Untuk soal di atas, karena F(x) berderajat 3 dan P(x) berderajat 2, maka
H(x) berderajat 3 – 2 = 1
S(x) berderajat 2 – 1 = 1
Jadi, misalkan H(x) = ax + b dan S(x) = cx + d
Maka:
2x³ – 3x² + x + 5 = (2x² – x – 1).(ax + b) + (cx + d)
Ruas kanan:
= 2ax³ + 2bx² – ax² – bx – ax – b + cx + d
= 2ax³ + (2b – a)x² + (–b – a + c)x + (–b + d)
Samakan koefisien ruas kiri dan ruas kanan:
x³ → 2 = 2a → a = 2/2 = 1
x² → –3 = 2b – a → 2b = –3 + a = –3 + 1 = –2 → b = –2/2 = –1
x → 1 = –b – a + c → c = 1 + b + a = 1 – 1 + 1 → c = 1
Konstanta → 5 = –b + d → d = 5 + b = 5 – 1 → d = 4
Jadi:
H(x) = ax + b = 1.x – 1 = x – 1
S(x) = cx + d = 1.x + 4 = x + 4

Teorema Faktor

Suatu suku banyak F(x) mempunyai faktor (x – k) jika F(k) = 0 (sisanya jika dibagi dengan (x – k) adalah 0)
Catatan: jika (x – k) adalah faktor dari F(x) maka k dikatakan sebagai akar dari F(x)
Tips:

1. Untuk mencari akar suatu suku banyak dengan cara Horner, dapat dilakukan dengan mencoba-coba dengan angka dari faktor-faktor konstantanya ang akan memberikan sisa = 0
2. Jika jumlah koefisien suku banyak = 0, maka pasti salah satu akarnya adalah x = 1
3. Jika jumlah koefisien suku di posisi genap = jumlah koefisien suku di posisi ganjil, maka pasti salah satu akarnya adalah x = –1

Contoh:
Tentukan penyelesaian dari x³ – 2x² – x + 2 = 0
Faktor-faktor dari konstantanya, yaitu 2,  adalah ±1 dan ±2
Karena jumlah seluruh koefisien + konstantanya = 0 (1 – 2 – 1 + 2 = 0), maka, pasti x = 1 adalah salah satu faktornya, jadi:


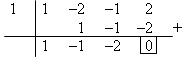
Jadi x³ – 2x² – x + 2 = (x – 1)(x² – x – 2)
= (x – 1)(x – 2)(x + 1)
x = 1   x = 2   x = –1
Jadi himpunan penyelesaiannya: {–1, 1, 2}

Sifat Akar-Akar Suku Banyak

Pada persamaan berderajat 3:
ax³ + bx² + cx + d = 0 akan mempunyai akar-akar x₁, x₂, x₃
dengan sifat-sifat:

• Jumlah 1 akar: x₁ + x₂ + x₃ = – b/a
• Jumlah 2 akar: x₁.x₂ + x₁.x₃ + x₂.x₃ = c/a
• Hasil kali 3 akar: x₁.x₂.x₃ = – d/a

Pada persamaan berderajat 4:
ax⁴ + bx³ + cx² + dx + e = 0 akan mempunyai akar-akar x₁, x₂, x₃, x₄
dengan sifat-sifat:

• Jumlah 1 akar: x₁ + x₂ + x₃ + x₄ = – b/a
• Jumlah 2 akar: x₁.x₂ + x₁.x₃ + x₁.x₄ + x₂.x₃ + x₂.x₄ + x₃.x₄ = c/a
• Jumlah 3 akar: x₁.x₂.x₃ + x₁.x₂.x₄ + x₂.x₃.x₄ = – d/a
• Hasil kali 4 akar: x₁.x₂.x₃.x₄ = e/a

Dari kedua persamaan tersebut, kita dapat menurunkan rumus yang sama untuk persamaan berderajat 5 dan seterusnya
(amati pola:  –b/a, c/a, –d/a , e/a, …)

Pembagian Istimewa

Persamaan Parabola


Seperti pada elips dan hiperbola, banyak sekali aplikasi parabola yang bertumpu pada definisi analitisnya daripada bentuk aljabarnya. Aplikasi-aplikasi tersebut, misalkan pembangunan teleskop radio dan perusahaan lampu senter, menggunakan definisi analitis parabola dalam penentuan lokasi fokus dari parabola tersebut. Berikut ini definisi analitis dari suatu parabola.

Definisi Parabola
Diberikan suatu titik tertentu f dan garis tertentu D dalam bidang, suatu parabola adalah himpunan semua titik (x, y) sedemikian sehingga jarak antara f dan (x, y) sama dengan jarak antara D dan (x, y). Titik f disebut sebagai fokus parabola dan garis D disebut sebagai direktriks.

Persamaan umum dari suatu parabola dapat diperoleh dengan mengkombinasikan definisi di atas dan rumus jarak. Dengan tidak mengurangi keumuman, kita dapat menganggap parabola yang ditunjukkan pada gambar di atas memiliki titik puncak di (0, 0) dan memiliki titik fokus di (0, p). Seperti yang ditunjukkan oleh gambar di bawah, parabola yang dimaksud memiliki direktriks dengan persamaan y = –p , sehingga semua titik pada D dapat dituliskan sebagai (x, –p).

Dengan menggunakan rumus jarak dan menerapkan definisi bahwa d1 = d2, kita mendapatkan,

Persamaan terakhir di atas disebut persamaan bentuk fokus-direktriks dari suatu parabola vertikal dengan titik puncak di (0, 0). Jika parabola di atas diputar sehingga terbuka ke kanan, maka kita akan mendapatkan suatu parabola horizontal dengan titik puncak di (0, 0), dan persamaannya adalah y² = 4px.

Persamaan Parabola dalam Bentuk Fokus-Direktriks
Suatu parabola vertikal memiliki persamaan dalam bentuk fokus-direktriks: x² = 4py, yang memiliki fokus di (0, p) dan dengan direktriks: y = –p. Jika p > 0, parabola tersebut akan terbuka ke atas. Jika p < 0, parabola tersebut akan terbuka ke bawah.
Suatu parabola horizontal memiliki persamaan dalam bentuk fokus-direktriks: y² = 4px, yang memiliki fokus di (p, 0) dan dengan direktriks: x = –p. Jika p > 0, parabola tersebut akan terbuka ke kanan. Jika p < 0, parabola tersebut akan terbuka ke kiri.

Untuk lebih memahami mengenai persamaan suatu parabola dalam bentuk fokus-direktriks, perhatikan contoh berikut.

Contoh 1: Menentukan Fokus dan Direktriks dari suatu Parabola

Tentukan titik puncak, fokus, dan direktris dari parabola yang didefinisikan oleh persamaan x² = –12y. Kemudian gambarkan grafiknya, disertai dengan fokus dan direktrisnya.

Pembahasan Karena hanya suku-x yang dikuadratkan dan tidak ada pergeseran yang diterapkan, maka parabola tersebut merupakan parabola vertikal dengan titik puncak di (0, 0). Dengan membandingkan persamaan yang diberikan dengan persamaan umum parabola bentuk fokus-direktriks kita dapat menentukan nilai p:

Karena p = –3 (p < 0), maka parabola tersebut terbuka ke bawah, dengan titik fokus di (0, –3) dan direktriksnya y = 3. Untuk menggambar grafiknya, kita perlu beberapa titik tambahan yang dilalui oleh parabola tersebut. Karena 36 = 6² dapat dibagi oleh 12, maka kita dapat mensubstitusikan x = 6 dan x = –6, dan menghasilkan titik-titik (6, –3) dan (–6, –3). Sehingga grafik dari parabola tersebut dapat digambarkan sebagai berikut.

Dari grafik di atas, kita dapat mengetahui bahwa garis x = 0 merupakan sumbu simetri dari grafik parabola yang diberikan.

Sebagai titik-titik alternatif dalam menggambar grafik parabola, kita dapat menggunakan apa yang disebut tali busur fokus dari parabola. Serupa dengan elips dan hiperbola, tali busur fokus adalah ruas garis yang melalui fokus, sejajar dengan direktriks, dan titik-titik ujungnya terletak pada grafik. Dengan menggunakan definisi dari parabola, jarak horizontal dari f ke (x, y) adalah 2p. Karena d1 = d2, maka ruas garis yang sejajar dengan direktriks dari fokus ke grafik memiliki panjang |2p|, dan panjang tali busur fokus dari sembarang parabola adalah |4p|.

Dan akhirnya, jika titik puncak dari suatu parabola vertikal digeser ke (h, k), maka persamaan dari parabola tersebut akan menjadi (x ± h)2 = 4p(y ± k). Seperti pada keluarga irisan kerucut lainnya, pergeseran vertikal dan horizontalnya berlawanan dengan tandanya (positif atau negatif).

Contoh 2: Menentukan Fokus dan Direktriks dari suatu Parabola

Tentukan titik puncak, fokus, dan direktriks dari persamaan parabola yang diberikan, kemudian gambarkan grafiknya, disertai dengan fokus dan direktriksnya: x² – 6x + 12y – 15 = 0.

Pembahasan Karena hanya suku-x yang dikuadratkan, maka grafik dari persamaan tersebut berbentuk parabola vertikal. Untuk menentukan kecekungan, titik puncak, fokus, dan direktriks, kita terlebih dulu melengkapkan kuadrat dalam x dan membandingkannya dengan persamaan bentuk fokus-direktriks dengan pergeseran.

Dari persamaan yang dihasilkan, kita dapat melihat bahwa grafiknya merupakan suatu parabola yang digeser ke kanan sejauh 3 satuan dan ke atas sejauh 2 satuan. Oleh karena itu, semua unsur dari parabola tersebut juga akan bergeser. Karena kita mendapatkan 4p = –12, maka p = –3 (p < 0) dan parabola tersebut terbuka ke bawah. Jika parabola tersebut berada pada posisi biasa, maka titik puncaknya akan di (0, 0), fokusnya di (0, –3), dan direktriksnya y = 3. Karena parabola tersebut bergeser ke kanan sejauh 3 satuan dan ke atas sejauh 2 satuan, maka kita harus menambahkan nilai x dengan 3 dan nilai y dengan 2 dari semua unsur parabola tersebut. Sehingga titik puncaknya akan berada di (0 + 3, 0 + 2) = (3, 2), fokusnya pada (0 + 3, –3 + 2) = (3, –1), dan direktriksnya adalah y = 3 + 2 = 5. Dan akhirnya, jarak horizontal antara fokus dan grafik adalah |2p| = 6 satuan (karena |4p| = 12), sehingga memberikan titik-titik tambahan yang dilalui grafik, yaitu (–3, –1) dan (9, –1).

Dalam banyak kasus, kita perlu untuk menentukan persamaan dari parabola ketika hanya beberapa informasi yang diketahui, seperti yang dicontohkan oleh contoh 3 berikut.

Contoh 3: Menentukan Persamaan dari suatu Parabola

Tentukan persamaan dari parabola yang memiliki titik puncak (4, 4) dan fokus (4, 1). Kemudian gambarkan grafiknya dengan menggunakan persamaan dan tali busur fokusnya.

Pembahasan Karena titik puncak dan fokusnya terletak pada garis vertikal, maka parabola yang dimaksud merupakan suatu parabola vertikal yang memiliki persamaan umum (x ± h)² = 4p(y ± k). Jarak p dari fokus ke titik pusat adalah 3 satuan, dan karena fokus berada di bawah titik puncak, maka grafiknya terbuka ke bawah dan p = –3. Dengan menggunakan tali busur fokus, jarak horizontal dari fokus ke grafik adalah |2p| = |2(–3)| = 6, memberikan titik-titik (–2, 1) dan (10, 1). Titik puncaknya digeser 4 satuan ke kanan dan 4 satuan ke atas dari (0, 0), sehingga diperoleh h = 4 dan k = 4. Sehingga persamaan dari parabola tersebut adalah (x – 4)² = –12(y – 4), dengan direktriks y = 7. Grafik dari parabola tersebut dapat digambarkan sebagai berikut.

Perhatikan bahwa grafik parabola di atas memiliki sumbu simetri di garis x = 4